10Sort
Sort 排序算法
[TOC]
1、冒泡排序
冒泡排序算法的运作如下:(从后往前)
① 比较相邻的元素。如果第一个比第二个大,就交换他们两个。 ② 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。 ③ 针对所有的元素重复以上的步骤,除了最后一个。 ④ 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较.
代码
void popSort(int *p, int n)
{
int tmp;
for(int i= n-1; i>0; i--)
{
for(int j=0; j<i; j++)
{
if(p[j] > p[j+1])
{
tmp = p[j];
p[j] = p[j+1];
p[j+1] = tmp;
}
}
}
}
优化版本
void popSort(int *p,int n)
{
int flag;
for (int i = 0; i < n-1; i++)
{
flag = 0; // 每一轮比较前都要设置标置位
for (int j = 0; j < n -i- 1; j++)
{
if (p[j] > p[j + 1])
{
p[j] = p[j]^p[j+1];
p[j+1] = p[j]^p[j+1];
p[j] = p[j]^p[j+1];
flag = 1;
}
}
if(flag == 0)
break;
}
}
评价
优点 : 稳定
缺点 :慢、每次只能移动两个数据
平均复杂度: O(n^2)
2、插入排序
插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置,直到全部插入完毕。
代码
void insertSort(int *a,int n)
{
int i,j,key;
for(i=1;i<n;i++) //控制需要插入的元素
{
key = a[i]; //key 为要插入的元素
//查找要插入的位置,循环结束,则找到插入位置
for(j=i; j-1>=0 && a[j-1]>key; j--)
{
a[j] = a[j-1]; //移动元素的位置.供要插入元素使用
}
a[j] = key; //插入需要插入的元素
}
}
评价
优点 : 稳定、快
缺点 :比较次数不一定,比较次数越少,插入点后的数据移动越多
平均复杂度: O(n^2)
3、希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 DL. Shell 于1959 年提出而得名。希尔的本质,是减少趟数和每趟比较的次数。
图示
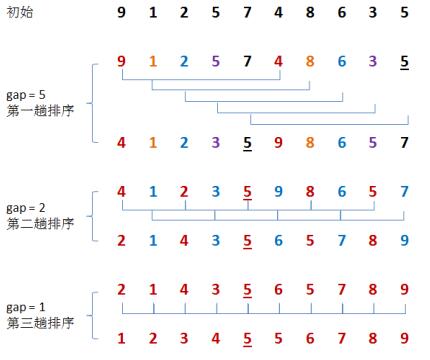
先取一个小于 n 的整数 d1 作为第一个增量,把文件的全部记录分组。所有距离为d1 的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量 d2 < d1 重复上述的分组和排序,直至所取的增量 =1(dn < … < d2 < d1 ),即所有记录放在同一组中进行直接插入排序为止。 一般的初次取序列的一半为增量,以后每次减半, 直到增量为 1。
① 在第一趟排序中,我们不妨设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。 ② 接下来,按照直接插入排序的方法对每个组进行排序。在第二趟排序中,我们把上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为 2 组。 ③ 按照直接插入排序的方法对每个组进行排序。在第三趟排序中,再次把 gap 缩小一半,即 gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成 1 组,即只有一组。 ④ 有多少组,即执行多少组的插入排序。
代码
void shellSort(int *p, int n)
{
int gap =n/ 2;
while (gap >= 1)
{
// 把距离为 gap 的元素编为一个组,扫描所有组
int i,j,key;
for ( i = gap; i < n; i++)
{
key = p[i];
// 对距离为 gap 的元素组进行排序
for (j = i; j-gap >=0 && p[j-gap] > key ; j = j - gap)
{
p[j] = p[j-gap];
}
p[j] = key;
}
gap = gap / 2; // 减小增量
}
}
评价
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
优点 : 快、移动数据少
插入排序在几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
缺点 :不稳定、d的取值是多少,应取多少个不同的值,都无法确切知道,只能凭经验来取。
平均复杂度: O(n^1.3)
4、选择排序
图示:
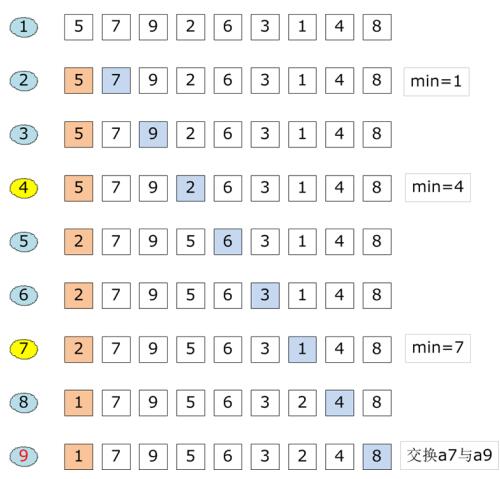
逻辑
① 第 1 趟,在待排序记录 r[0]~r[n]中选出最小的记录,将它与 r[0]交换; ② 第 2 趟,在待排序记录 r[1]~r[n]中选出最小的记录,将它与 r[1]交换; ③ 以此类推,第 i 趟在待排序记录 r[i]~r[n]中选出最小的记录,将它与 r[i]交换,使有序序列不断增长直
到全部排序完毕。
代码
int selectSort(int *p, int n)
{
for(int i=0; i<n-1; i++)
{
for(int j=i+1; j<n; j++)
{
if(p[i]>p[j])
{
p[i] ^= p[j];
p[j] ^= p[i];
p[i] ^= p[j];
}
}
}
}
评价
优点 : 移动数据的次数已知(n-1次)
缺点 :比较次数多
平均复杂度: O(n^2)
优化
#include <iostream>
using namespace std;
int selectSort(int *p, int n)
{
int idx;
for(int i=0; i<n-1; i++)
{
idx = i;
for(int j=idx+1; j<n; j++)
{
if(p[idx] >p[j])
idx = j;
}
if(idx != i)
{
p[i] ^= p[idx];
p[idx] ^= p[i];
p[i] ^= p[idx];
}
}
}
int main()
{
int arr[10] = {1,2,3,4,5,0,9,8,7,6};
selectSort(arr,10);
for(int i=0; i<10; i++)
{
printf("%d\n",arr[i]);
}
return 0;
}
5、快速排序
快速排序是 一种划分交换排序。采用了一种分治的策略,通常称其为分治法(Divide-and-Conquer Method)。
图示
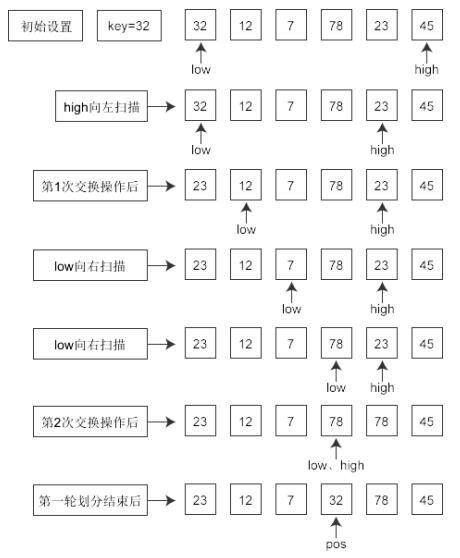
逻辑 ① 先从数列中取出一个数作为基准数(通常取第一个数)。 ② 分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。 ③ 再对左右区间重复第二步,直到各区间只有一个数。
代码
void quickSort(int *p, int left, int right)//数字代表下标
{
if(left < right)
{
int pivot = p[left];
int low = left; int high = right;
while(low<high)
{
while(p[high]>=pivot && low<high)
{
high--;
}
p[low] = p[high];
while(p[low] <=pivot && low<high)
{
low++;
}
p[high] = p[low];
}
p[low] = pivot;
quickSort(p,left,low-1);
quickSort(p,low+1,right);
}
}
评价
优点 : 极快、移动数据少
缺点 :不稳定,递归
平均复杂度: O(nlogn)
6、归并排序(常见的面试题)
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
图示:
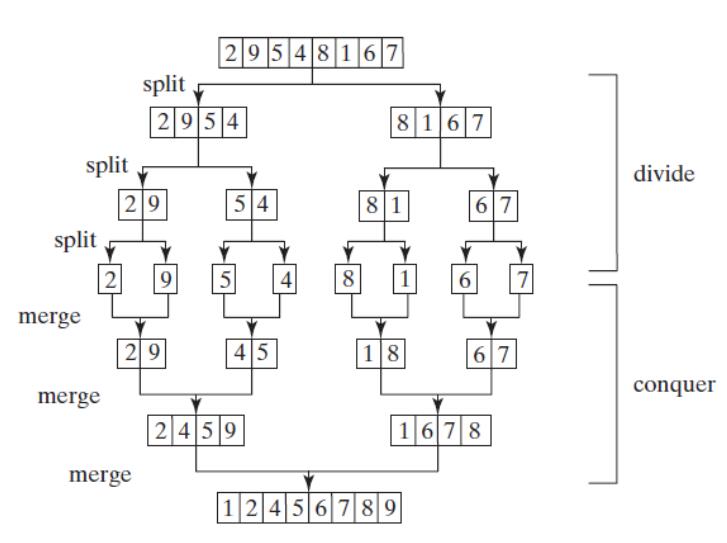
逻辑 ① 将序列每相邻两个数字进行归并操作(merge),形成 floor(n/2)个序列,排序后每个序列包含两个元素 ② 将上述序列再次归并,形成 floor(n/4)个序列,每个序列包含四个元素 ③ 重复步骤 2,直到所有元素排序完毕
代码
#include<iostream>
using namespace std;
//==========归并排序==========//
//==========两个有序数组合并为一个数组==========//
void mergeArrTest(int *firstArr, int numfirst, int *secondArr, int numsecond, int *mergeArr, int mergenum)
{
int iFirst = 0; int jSecond = 0; int kMerge = 0;
while (iFirst != numfirst && jSecond != numsecond)
{
//升序
if (firstArr[iFirst] > secondArr[jSecond])
mergeArr[kMerge++] = secondArr[jSecond++];
else
mergeArr[kMerge++] = firstArr[iFirst++];
}
if (iFirst == numfirst)
while (jSecond != numsecond)
mergeArr[kMerge++] = secondArr[jSecond++];
if (jSecond == numsecond)
while (iFirst != numfirst)
mergeArr[kMerge++] = firstArr[iFirst++];
}
//==========合并同一有序数组==========//
void mergeArr(int *sourceArr, int *mergeTempArr, int startIdx, int midIdx, int endIdx)
{
int i = startIdx; int j = midIdx + 1; int k = startIdx;
while (i != midIdx + 1 && j != endIdx + 1)
{
if (sourceArr[i] > sourceArr[j])
mergeTempArr[k++] = sourceArr[j++];
else
mergeTempArr[k++] = sourceArr[i++];
}
if (i == midIdx +1)
while (j != endIdx + 1)
mergeTempArr[k++] = sourceArr[j++];
if (j == endIdx+1)
while (i != midIdx + 1)
mergeTempArr[k++] = sourceArr[i++];
while (startIdx != endIdx+1)
{
sourceArr[startIdx] = mergeTempArr[startIdx];
startIdx++;
}
}
//归并排序
void mergeSort(int *src, int *tmp, int start, int end)
{
if (start < end)
{
int mid = (start + end) / 2;
mergeSort(src, tmp, start, mid);
mergeSort(src, tmp, mid + 1, end);
mergeArr(src, tmp, start, mid, end);
}
}
int main()
{
/*
int firstArr[10] = { 1, 3, 5, 7, 9, 11, 33,55, 77, 99 };
int secondArr[5] = { 2, 4, 6, 8,9 };
int mergeArr[15];
mergeArrTest(firstArr, 10, secondArr, 5, mergeArr, 15);//两个有序数组合并为一个数组//
for (int i = 0; i<15; i++)
{
printf("%d\n", mergeArr[i]);
}
*/
/*
int sourceArr[10] = { 1, 3, 5, 7, 9, 2, 4, 6, 8, 10 };//====合并同一有序数组=====//
int mergetmpArr[10];
int startidx = 0; int endidx = 9;
int mididx = (startidx + endidx)/2;
mergeArr(sourceArr, mergetmpArr, startidx, mididx, endidx);
for (int i = 0; i<10; i++)
{
printf("%d\n", mergetmpArr[i]);
}
*/
int Arr[10] = { 1, 4, 8, 3, 6, 9, 0, 2, 5, 7 };
int Arr3[10];
mergeSort(Arr, Arr3,0, 9);
for (int i = 0; i<10; i++)
{
printf("%d\n", Arr3[i]);
}
return 0;
}
归并排序是稳定的排序.即相等的元素的顺序不会改变.如输入记录 1(1) 、3(2)、2(3) 、2(4) 、5(5) (括号中是记录的关键字)时输出的 1(1) 、2(3)、 2(4) 、3(2)、 5(5) 中的 2 和 2 是按输入的顺序.这对要排序数据包含多个信息而要按其中的某一个信息排序,要求其它信息尽量按输入的顺序排列时很重要.这也是它比快速排序优势的地方.需要额外空间,故称为外排序,前面讲的都是内排序,比如冒泡等。
评价
优点 : 稳定,效率高
缺点 :外排序
平均复杂度: O(nlogn)
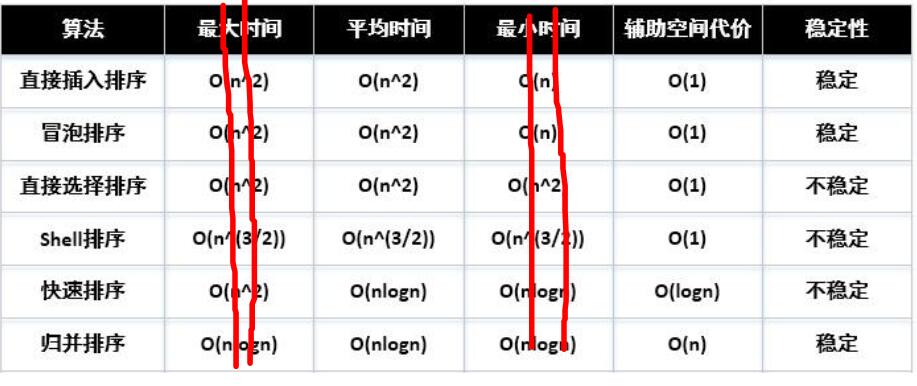
算法小结